| Lower / Upper triangular matrix(하 / 상삼각행렬) | (대각선을 포함해) 각각 아래 / 위쪽 행렬만 값이 있고, 나머지는 0인 행렬. 줄여서 L / U로 표현한다. |
 |
우선 transpose(전치)라는 간단한 개념을 살펴보자.

어떤 행렬 A에 대해, 그 row와 column의 원소들을 바꿔 준 행렬이 바로 A의 전치 행렬이다. 윗 첨자 T를 통해 표현한다. 이 전치 행렬은 다음과 같은 다양한 성질들이 있다.
1) 우리가 역행렬의 개념을 정의할 때 아래와 같은 식을 사용했다.

위 식을 전치하면, 아래와 같이 곱하는 순서가 뒤바뀐다.

2) 역행렬과 전치행렬간 교환 법칙이 성립한다. 단 이는 각각의 단일 행렬에게만 적용된다.

matrix decompostion은 "분해"라는 번역명에 걸맞게 행렬 하나를 여러 작은 행렬의 곱으로 나타내는 것을 의미한다.



개념 자체는 굉장히 간단하지만, 왜 굳이 멀쩡한 행렬을 수고스럽게 쪼개는 행위를 하는지는 여전히 의문스러울 것이다. 몇 가지 이유가 있겠지만, 가장 대표적인 이유로는 연립방정식을 더욱 쉽게 풀이할 수 있게 되기 때문이다.
이번 포스팅에서는 다음 연립방정식을 변형한 행렬 A를 대상으로 LU decomposition을 알아볼 것이다..


1) LU-Decomposition (LU 분해)
어떤 행렬 A를 Lower matrix와 Upper matrix의 곱으로 분해한다. A=LU

좌변의 행렬 A를 우변처럼 두 삼각행렬로 만들어야 한다. 차근차근 단계별로 진행해 보자.
1) L행렬 : 우선 단위행렬을 만들어 둔다. U행렬 : A와 동일하게 둔다.

계속 문자를 쓰기 번거로우니 아래의 예시로 A행렬의 원소들을 대체하겠다.
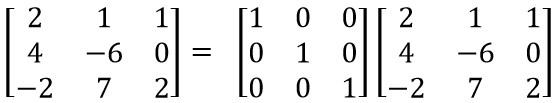
2) 이제 우리의 지상과제는, U행렬을 U행렬에 걸맞게 좌하단 값을 0으로 만드는 일이다. 우선 1열 2행의 값인 4를 0으로 만들어야 하는데, 이를 위해 1행에 특정 상수 a를 곱한 값들을 2행에서 빼주고, 이 a가 L행렬의 1열 2행에 들어간다.
4-2*a = 0이므로 상수 a = 2가 된다.

위 식에서 , a는 4-a*2 = 0 을 충족해야 하므로, a = 2이다.

3) 원리를 알았으니 다음은 간단하다. U행렬의 1열 3행의 값인 -2를 0으로 만드는 a가 필요한데, -2-a*2 = 0 이므로 이번 상수의 값은 a = -1이다. 이 값 역시 L행렬의 1열 3행에 들어가게 된다.

이번엔 U행렬의 2열 3행의 값인 8을 0으로 만들어야 한다. 2열의 경우 2행의 값들을 대상으로 하며, 8-a*(-8) = 0 이므로 이번 a는 -1이다.

여기까지가 LU decomposition의 과정이다. 다음은 이를 통해 연립방정식을 푸는 과정이다.
아래와 같은 연립방정식은, LU decomposition을 통해 그 아래로 분해된다.

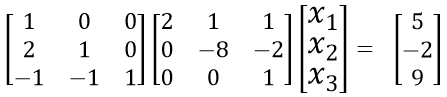
위 행렬은 아래와 같이 합쳐질 수 있다.

이 연립방정식은 굉장히 풀기 쉽다.
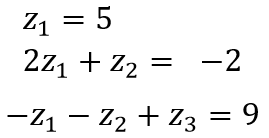
z1 = 5임이 바로 나오기 때문에 z2= -12, z3=2 또한 바로 계산된다. 이제 앞서 z로 합쳤던 값들도 풀 수 있다.


x3 =2로부터 x2 = 1, x1 = 1 또한 계산해낼 수 있다. 지금이야 간단한 연립방정식을 푸니 더 번거롭게 느껴질 수 있지만, 더 복잡한 방정식의 경우 LU decomposition을 통해 더 쉽게 풀 수 있게 될 것이다.
'수치해석' 카테고리의 다른 글
| QR decomposition, GS process, Householder reflection (0) | 2022.05.04 |
|---|---|
| LU Decomposition (0) | 2022.04.22 |
| 행렬 - linear transformation (0) | 2022.04.17 |
| 행렬 - condition number(조건수) (0) | 2022.04.15 |
| Eigenvalue & Eigenvector (0) | 2022.04.15 |

