행렬 - linear transformation

기저 벡터(basis vector)

n차원 공간에서 기준이 되는 벡터. 좌표평면에서의 x / y /z와 비슷하게 벡터의 기준이 되는 값이다. 보통 i,j,k...순으로 표기한다.

 

행렬에 있어 변환(transformation)이란, 함수의 개념으로 이해하면 쉽다. f(x) = 3x라는 함수에서, x라는 값을 입력하면 3x가 출력되는 것과 같이 변환 또한 어떤 벡터를 입력하면 새로운 백터를 출력시켜 준다. 

 

단, 2차원 평면에 나타내는 방식은 함수와는 조금 다르다. 2차원 평면에서 함수는 f(x) = ax와 같이 하나의 실선으로 나타나지만, 변환의 경우 어떤 벡터이던지 대입할 수 있기 때문에 실선으로 표현하자면 무수히 많은 실선이 필요하게 되고, 따라서 그래프의 모습으로 표기하는 대신 좌표의 격자를 변화시키는 방식으로 표현한다.

y=3x의 그래프

수많은 벡터 별로 각기 다른 결과값이 나오기 때문에 격자의 변화된 모습으로 나타낸다.

이 때 변화된 격자와 함께 기존 격자(회색)를 남겨두면 비교가 더 쉬워진다. 아래의 예시들과 같이 다양한 변환들이 존재한다.

 

보기에는 예쁘지만 전혀 공부하고 싶은 마음이 들지 않는 변환들이다. 다행스럽게도, 위와 같은 변형들은 비선형 변환(Nonlinear Transform)으로, 우리가 공부하게 될 선형 변환(Linear transform)과는 다른 종류의 변환이다.

 

선형 변환은 다음과 같은 특징이 있다. 

1) 변환 후 격자가 직선을 유지한다(휘지 않는다).

2) 변환 후에도 직선들이 일정한 간격으로, 평행하게 존재한다

2) 원점의 위치가 변하지 않는다.

 

마지막으로, 예시를 통해 선형 변환의 방법을 알아보자.

노란색 (-1,2) 벡터가 선형변환을 통해 (5,2)로 변환되는 모습이다. 각각의 노란 벡터는 다음과 같이 기저벡터들의 선형결합으로 나타낼 수 있다.

변형 후의 기저벡터는 아래첨자 t를 통해 구분한다

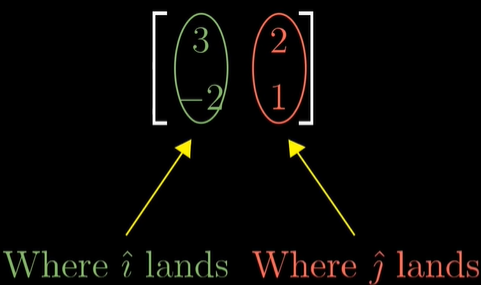
변환을 알아내는 방법은 단순하다. 기저벡터의 변화량을 알기만 하면 되기 때문이다. 위 예시에서, 기저벡터 i의 경우 변환 후 (1,-2)가 되었고, j의 경우 (3,0)이 되었다. 이 값들을 기존 벡터에 곱하면 변환 후의 값을 알 수 있게 된다.

위 식을 일반화시켜보자, 시작하는 노란 벡터의 좌표값을 (x,y)라고 하고, 기저벡터의 변화량을 각각 (a,b)와 (c,d)라고 한다면 위 식은 아래와 같이 일반화 할 수 있다.

추가적으로, 이 i hat과 j hat의 변화량을 2x2 행렬로 나타내기도 한다. 

좌측이 i, 우측이 j에 해당한다.

 

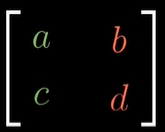
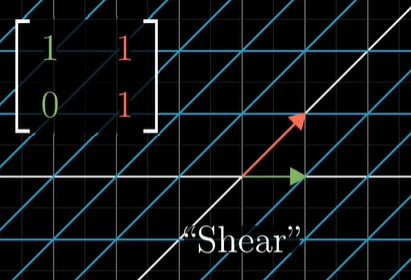
아래 몇 가지의 대표적인 선형 변환의 예시를 첨부해 두었다.

해당 행렬은 벡터를 반시계뱡향(counterclockwise)으로 90도 회전시킨다.

"Shear"라는 이름의 변환은 j hat의 위치만 (1,1)로 변화한다.

 

마지막으로 선형 변환의 특징인 선형성(Linearity)에 대해 알아보자. 선형성이란, 어떤 함수가 다음 두 가지 조건을 만족할 때 성립한다.

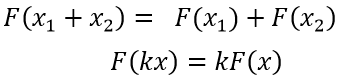
함수와 같은 방식으로 행렬의 선형성 또한 성립한다.

 

 

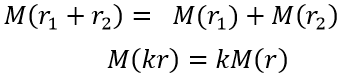
사진 출처 : 3Blue1BrownClips

https://youtu.be/kYB8IZa5AuE?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab