테일러 급수 간단하게 알아보기

분명 수학과 관련 없는 과를 선택하였지만 이상하게도 계속 마주치게 되는 테일러 급수(Taylor series 혹은 Taylor expansion)이다. 계속해서 피할 수는 없으니 간단하고 쉽게 이해해보도록 하자
핵심 개념은 "어떤 짜증나는 함수 A가 있을 때, 대신 비슷하게 생긴 쉬운 함수들을 더하다 보면 A와 비슷하게 만들 수 있지 않을까?"이다. 아래 두 예시가 있지만 귀찮다면 넘겨도 상관없다.
예시 1
1. 짜증 나게 생긴 e^(-x^2)의 그래프이다
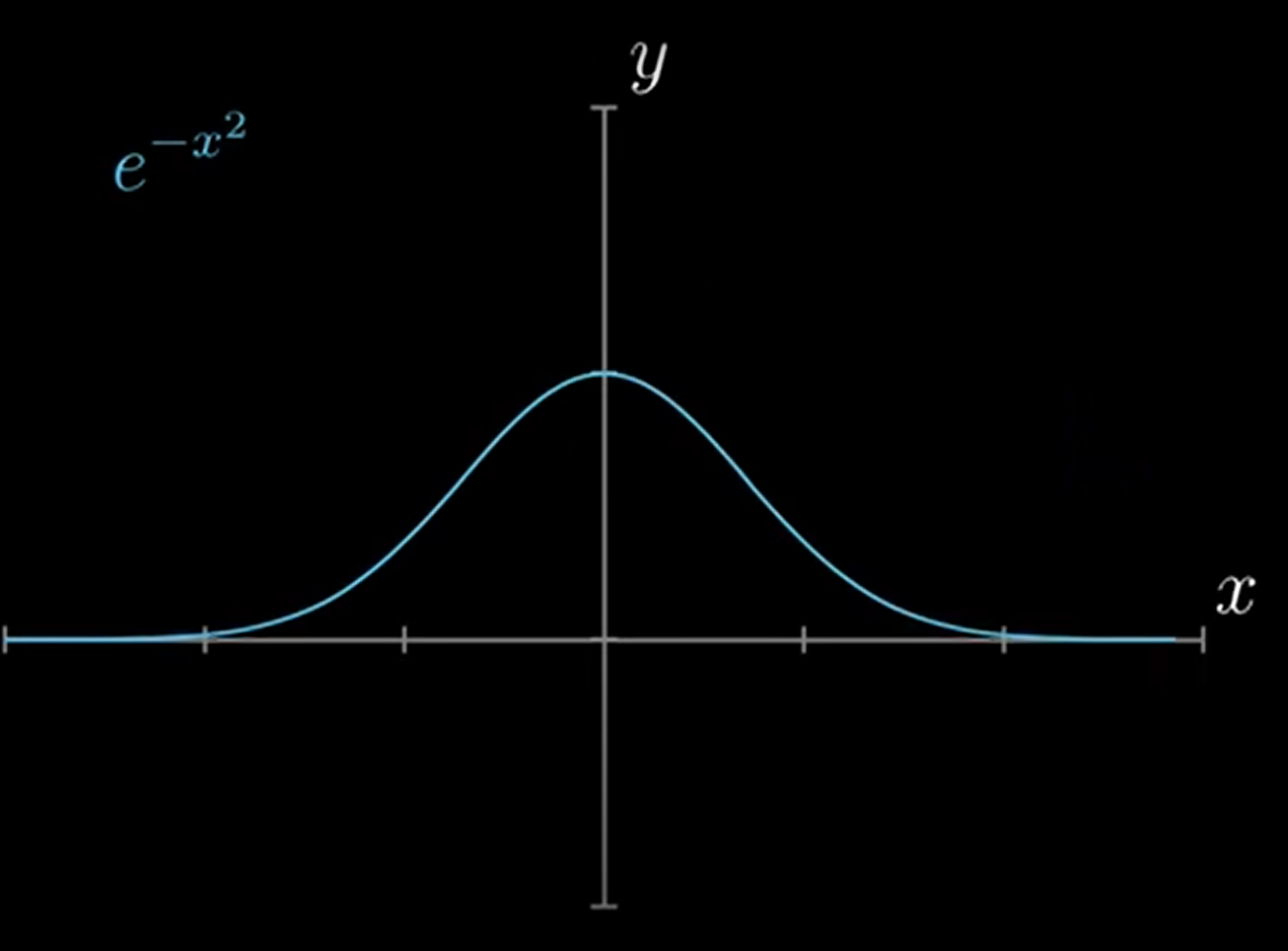
2. 친근하게 생긴 1-x^2 그래프를 가져다 대 보니, x=0 근처에서 모양이 비슷하다.
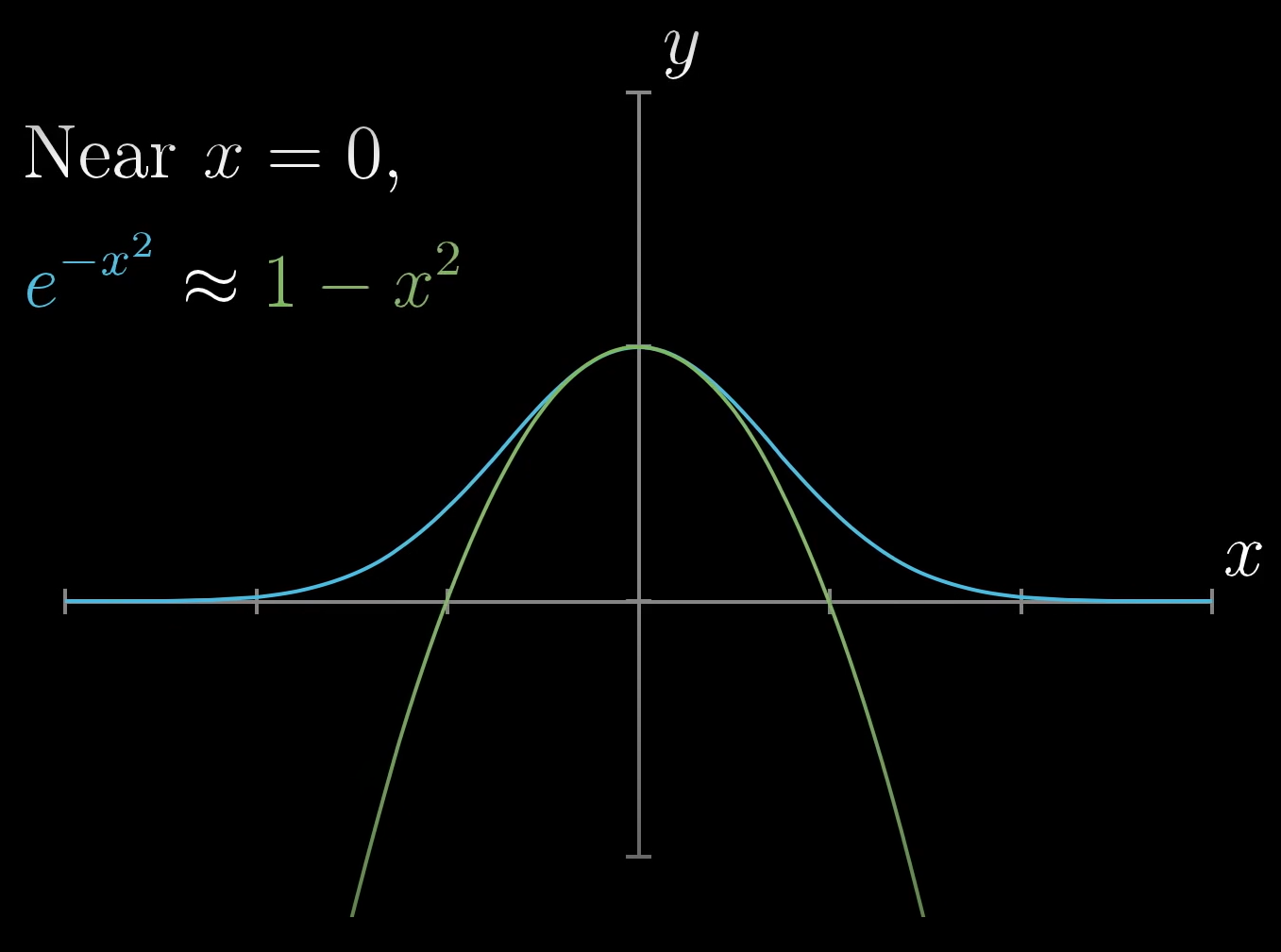
3. 여기 1/2 x^4를 더하니, 조금 더 먼 거리에서도 원래 함수와 비슷해졌다.
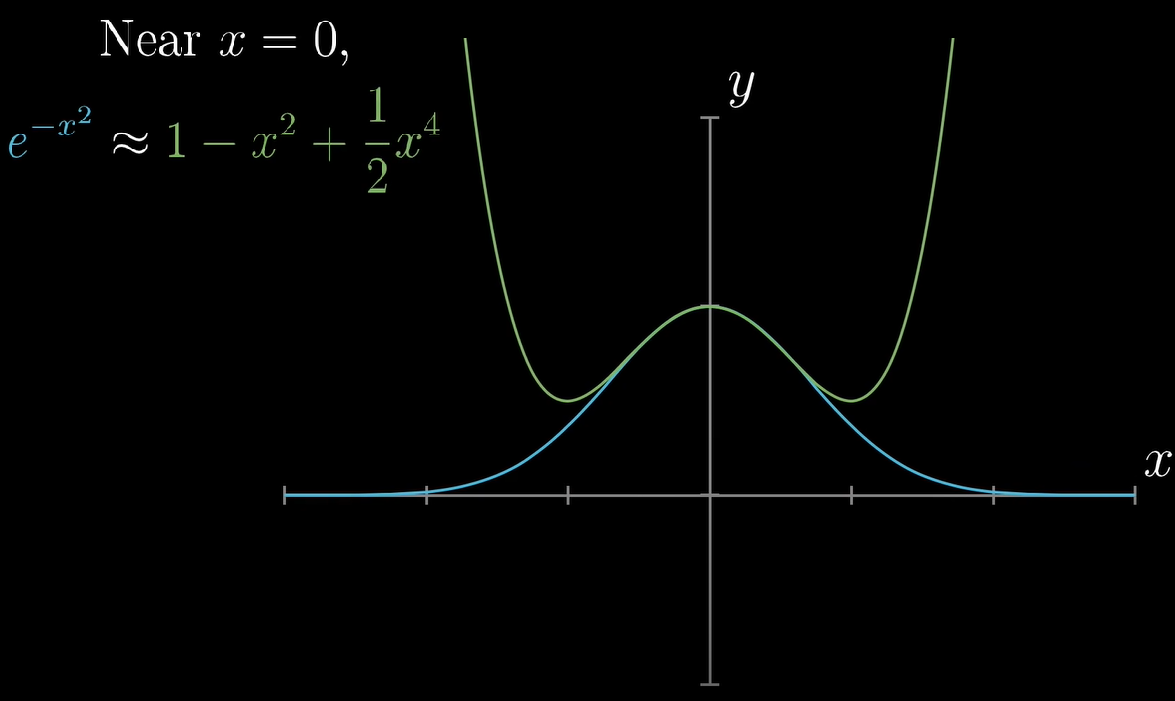
이를 계속 반복하다 보면 점점 본래의 그래프와 비슷해질 것이다.
예시 2
1. 이번 함수는 e^x이다. 앞서와 같이 x=0 근처에서는 (1+x) 그래프와 조금 비슷한 것 같기도 하다.
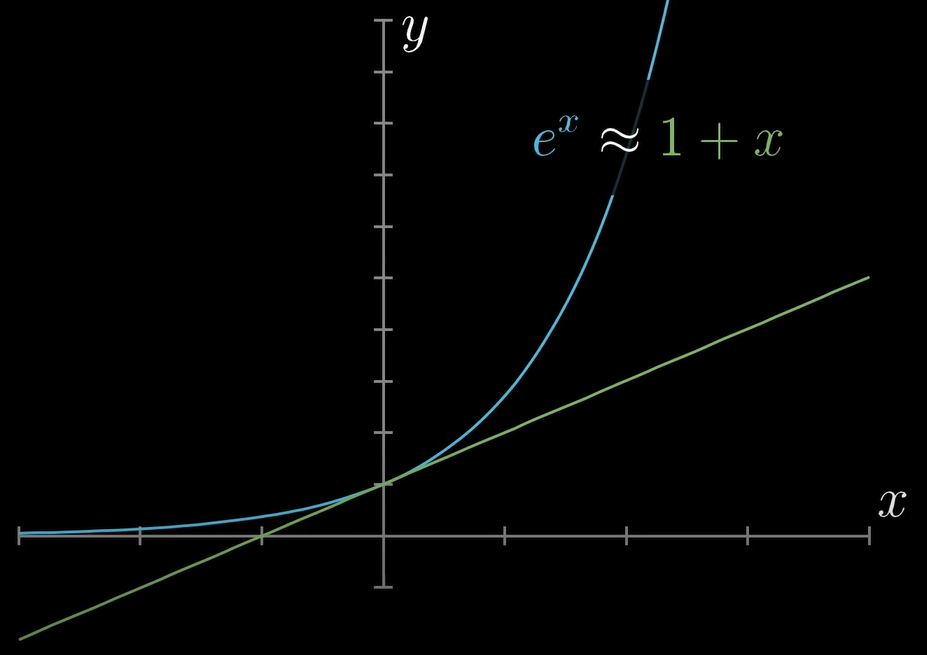
2. 다른 만만한 함수들을 계속 더하다 보니, 원본과 거의 유사해졌다!

개념을 이해했다면 진짜 정의를 통해 식에 대해 알아보자.
테일러 급수는 "주어진 함수를 특정 점의 미분계수들을 계수로 하는 무한급수(멱급수)로 표현된 함수로 나타내는 것"이라고 표현할 수 있다.
여기서 직관적으로 이해하기 어려운 부분은 "특정 점의 미분계수들을 계수로 하는 무한급수(멱급수)" 일 것이다. 하나씩 살펴보면,
-특정 점 : 위 예시들에서 x=0 비슷한 함수를 찾는 것부터 출발한 것을 볼 수 있다. "특정 점"을 0으로 설정한 것이다.
-미분계수들을 계수로 하는 무한급수 : 복잡한 내용이다. 축약하면, 특정 점과 그 점에서의 0,1,2,···차 도함수를 통해 접선의 방정식을 구해가는 과정인데, 계산 결과 아래 식의 무한급수가 된다.
-멱급수 : 아래의 무한급수가 바로 멱급수의 한 종류이다.
어쨌든 테일러 급수를 식으로 표현하면 결과적으로 아래와 같다.

a라는 값을 처음 보는 것 같지만 사실 우리가 이미 알고 있는 값이다. 바로 앞서 설명하였던 "특정 점"에 해당한다. 특히 앞서와 같이 a=0인 경우는 특별히 매클로린 급수(Maclaurin's series)라고 부른다.
분자에 해당하는 f^(n)(a)은 f의 n차 미분계수를 의미한다. n=0일 때 f(a), n=1일 때 f'(a) 그리고 n=2일 때 f''(a)와 같은 방식이다.
정의에서는 n을 무한대까지 끌고 가지만, 보통은 계산 상 편의를 위해 1~2차 항 정도까지만 계산한다. 이 정도만 해도 큰 오차가 발생하지는 않지만, 오차에 굉장히 민감한 경우에는 고차항까지 계산하기도 한다.
나름 간단히 정리한다고 정리했지만 그래도 복잡하게 느껴지는 테일러 급수이다. 그래도 기본 개념을 이해하고 있으면 테일러 급수를 만날 때마다 초면인 것 같은 기분은 더 이상 느끼지 않아도 되지 않을까 생각한다..
예시 그래프 출처: Youtube 3Blue1Brown